バーチ・スウィンナートン＝ダイアー予想とは？未解決の数学ミレニアム問題を徹底解説

はじめに

未解決の数学的難問として知られる「ミレニアム懸賞問題」の一つ、バーチ・スウィンナートン＝ダイアー予想（以下、BSD予想）をご存知でしょうか。この予想は、整数論の分野において極めて重要な位置を占めており、現代数学における未解明の領域を象徴する問題として広く認識されています。クレイ数学研究所が2000年に設定した7つのミレニアム懸賞問題のうちの一つに選ばれたこの予想は、その解決が数学の多様な分野に深い影響を及ぼすと期待されています。

本記事では、BSD予想の基本的な内容から、その背後にある楕円曲線やL関数の理論、そして現在の研究状況に至るまで、体系的に説明いたします。数学に詳しくない読者の方にも理解しやすいように、専門用語を丁寧に解説しながら進めます。また、BSD予想が持つ数学的意義や、それが解決された場合に予想される影響についても触れ、読者の皆様にこの問題の魅力をお伝えできれば幸いです。

1. バーチ・スウィンナートン＝ダイアー予想とは？

バーチ・スウィンナートン＝ダイアー予想は、整数論の中心的な研究対象である楕円曲線と、その性質を記述する解析的な道具であるL関数を結びつけるものです。この予想は、1960年代にイギリスの数学者ブライアン・バーチ（Bryan Birch）とピーター・スウィンナートン＝ダイアー（Peter Swinnerton-Dyer）によって提唱されました。彼らは、コンピュータを用いた数値実験を通じて、楕円曲線の有理点の個数とL関数の振る舞いの間に驚くべき関係があることを発見し、それを予想として定式化しました。

具体的には、BSD予想は以下のような主張をしています。「ある楕円曲線の有理点の個数（より正確には、そのランクと呼ばれる指標）は、その楕円曲線に対応するL関数が複素数平面の特定の点（s = 1）でどのように振る舞うかによって決定される」というものです。この主張は、数論という代数的構造を扱う分野と、解析学という連続的な手法を用いる分野を結びつけるものであり、その深遠さが多くの数学者を引きつけています。

BSD予想が解決されれば、楕円曲線の性質を解析的手法で完全に理解する道が開かれるだけでなく、数論全体の発展に革命的な影響を与えると考えられています。そのため、クレイ数学研究所は、この問題の解決に対して100万ドルの懸賞金を設定し、世界中の数学者に挑戦を呼びかけているのです。

2. 楕円曲線とは？

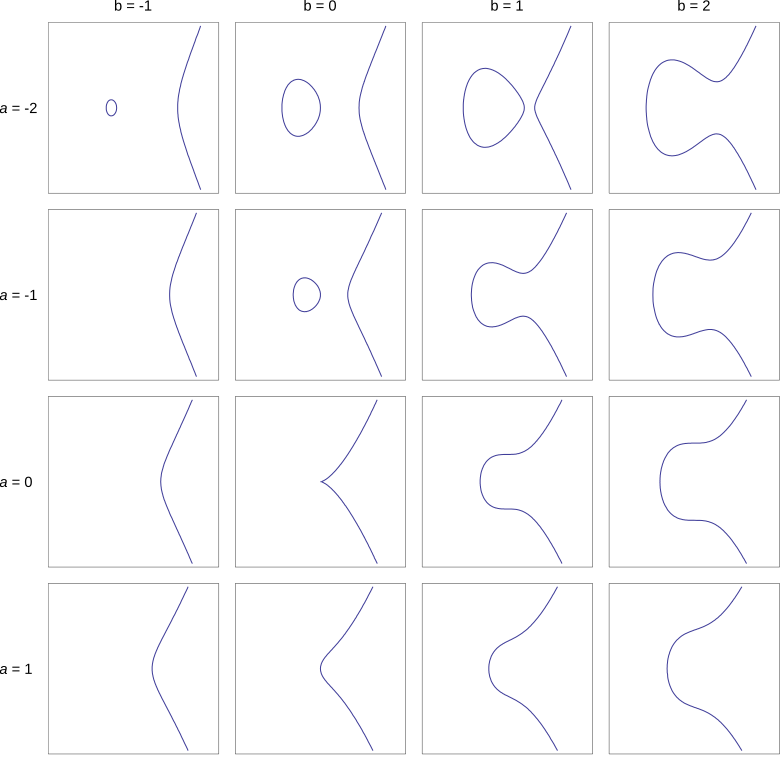
BSD予想を深く理解するためには、まずその主役である「楕円曲線」について知る必要があります。楕円曲線とは、数学において特定の形をした曲線を指し、特に整数論や代数幾何学の分野で重要な役割を果たします。以下にその定義と性質を詳しく説明いたします。

2.1 楕円曲線の定義

楕円曲線は、次のような3次方程式で表される曲線として定義されます。

$E : y^{2} = x^{3} + a x + b$

ここで、 $a$ と $b$ は実数や有理数などの係数であり、曲線が滑らかであるためには、次の判別式がゼロでないことが条件となります。

$Δ = 4 a^{3} + 27 b^{2} \neq 0$

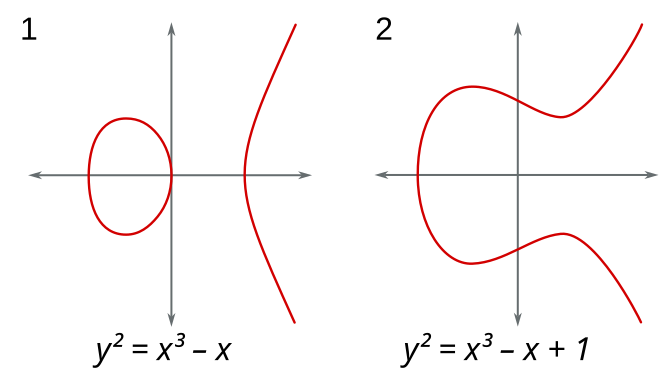
この条件が満たされると、曲線は特異点（尖った点や交差点）を持たず、滑らかな形状を描きます。たとえば、

$y^2 = x^3 – x$

や

$y^2 = x^3 – x + 1$

などが具体的な楕円曲線の例として挙げられます。これらの曲線は、グラフに描くと左右対称で、楕円形に似た形状を持つことが多いですが、厳密には「楕円」とは異なる数学的対象です。

2.2 楕円曲線の群構造

楕円曲線の最も興味深い性質の一つは、その点の集合が「群」を形成することです。具体的には、楕円曲線上の点に対して特別な加法演算を定義することができ、この演算によって点の集合が加法群としての性質を持つのです。この加法演算は幾何学的に定義され、以下のような手順で行われます。

１．曲線上の2点 $P$ と $Q$ を選び、それらを結ぶ直線を引きます。

２．その直線が楕円曲線と交わる3点目を $R^{}$ $R’$ とします。

$R’$ を $x$ 軸に関して対称に反転させた点を $R$ とし、これを $P + Q$ と定義します。

この演算により、楕円曲線上の点は「足し算」が可能な数学的構造を持ちます。さらに、「単位元」として曲線上の無限遠点を加え、逆元も定義されるため、完全な群となります。この群構造が、楕円曲線を整数論や暗号理論で重要な対象としている理由の一つです。

2.3 有理点の重要性

楕円曲線を研究する際、特に注目されるのは「有理点」です。有理点とは、座標

$(x, y)$

がともに有理数（分数で表される数）である点のことを指します。たとえば、方程式

$y^2 = x^3 – x$

において、点

$(0, 0)$

は

$x = 0, y = 0$

を満たすため有理点です。

有理点の個数が有限か無限か、またその構造がどのように決まるのかは、楕円曲線研究の中心的なテーマです。BSD予想は、この有理点の構造をL関数という解析的な道具で説明しようとする試みなのです。

3. 楕円曲線のランクと有理点

楕円曲線上の有理点の集合は、数学者ルイ・モーデル（Louis Mordell）が1920年代に証明した定理によって、次のように分類されます。

$E (Q) ≅ Z^{r} \times T$

ここで、 $E(\mathbb{Q})$ は楕円曲線 $E$ 上の有理点の群を表し、 $\mathbb{Z}^r$ は自由部分（整数を係数とする $r$ 次元の格子）、 $T$ は有限巡回群（ねじれ部分）を意味します。

3.1 ランクとは何か？

この式における

$r$

は「ランク（Rank）」と呼ばれ、楕円曲線の有理点の構造を決定する重要な指標です。

ランク $r$ は、独立な無限階の有理点の個数を表します。具体的には、次のように解釈されます。

$r = 0$ の場合、有理点は有限個しか存在せず、無限に多くの有理点は生成されません。
$r \geq 1$ の場合、少なくとも
$r$ 個の独立な有理点が存在し、それらを組み合わせることで無限個の有理点が得られます。

たとえば、ランクが1の場合、ある基本的な有理点 $P$ を見つけ、その整数倍（ $2P, 3P, \ldots$ ）を計算することで無限に多くの有理点が生成されます。

3.2 ねじれ点とは？

一方、有限巡回群

$T$

は「ねじれ点（Torsion Points）」を表します。ねじれ点とは、ある整数 $n$ を掛けることで無限遠点（群の単位元）に戻る点のことです。たとえば、

$nP = O$

（ $O$ は無限遠点）を満たす点がねじれ点です。モーデルの定理によれば、ねじれ点の個数は常に有限であり、その構造は楕円曲線ごとに異なります。

3.3 ランクの計算の難しさ

楕円曲線のランクを具体的に求めることは、非常に難しい問題です。現在の数学では、特定の楕円曲線に対してランクを計算するアルゴリズムが存在しますが、一般的な場合に適用できる完全な方法はまだ確立されていません。BSD予想は、このランクをL関数の性質から予測する手がかりを与えるものであり、その証明が待たれている理由の一つです。

4. L関数とBSD予想

BSD予想の核心は、楕円曲線に対応する「L関数」と呼ばれる解析的対象にあります。以下に、L関数の定義と、それがBSD予想でどのように関わってくるのかを説明いたします。

4.1 L関数の定義

楕円曲線

$E$

に対応するL関数は、次の無限積として定義されます。

$L (E, s) = \prod_{p 素数} {(1 - a_{p} p^{- s} + p^{1 - 2 s})}^{- 1}$

ここで、 $p$ は素数を動き、 $a_p$ は楕円曲線 $E$ の局所的な情報を反映する整数です。具体的には、

$a_p = p + 1 – N_p$

であり、 $N_p$ は素数 $p$ を法とした $E$ 上の点の個数を表します。このL関数は、複素数 $s$ の関数として定義され、解析的な性質を持つことが知られています。

L関数は、もともとリーマンゼータ関数やディリクレL関数の一般化として発展したもので、数論において重要な役割を果たします。楕円曲線のL関数は、特にその「モジュラー性」と呼ばれる性質により、深い数学的構造を持っています。

4.2 BSD予想の主張

BSD予想は、このL関数の特殊値

$L(E, 1)$

（ $s = 1$ における値）と、楕円曲線のランク

$r$

の間に次のような関係があると主張しています。

$L(E, 1) \neq 0$ のとき、ランク
$r = 0$ であり、有理点は有限個しか存在しません。
$L(E, 1) = 0$ のとき、ランク
$r \geq 1$ であり、無限個の有理点が存在します。
さらに、
$s = 1$ におけるL関数の零点の次数（すなわち、

$L(E, s)$ の導関数が何階まで消失するか）がランク

$r$ に一致します。

この関係は、数値実験によって初めて示唆され、その後多くの具体例で検証されています。しかし、一般的な楕円曲線に対してこの主張を厳密に証明することは、現代数学の最大の挑戦の一つとされています。

4.3 L関数の解析的性質

L関数の重要性は、その解析的な振る舞いにあります。たとえば、L関数が

$s = 1$

でゼロになる場合、その「消失の程度」（零点の次数）が楕円曲線の複雑さを反映していると考えられます。また、L関数は「関数等式」と呼ばれる対称性を持ち、これがBSD予想の深い背景を形成しています。このような性質は、楕円曲線とモジュラー形式の関係とも結びついており、後述する研究の進展でさらに詳しく触れます。

5. BSD予想の進展と未解決部分

BSD予想は、提唱されてから半世紀以上が経過し、多くの数学者によって研究が進められてきました。以下に、これまでの進展と残された課題について詳しく見ていきます。

5.1 既知の結果

BSD予想に関する研究は、次のような段階を経て進展してきました。

1970年代の部分証明: ジョン・コーツ（John Coates）とアンドリュー・ワイルズ（Andrew Wiles）らは、特定の条件を満たす楕円曲線に対してBSD予想の一部を証明しました。この結果は、「弱いBSD予想」と呼ばれ、ランクが0または1の場合にL関数の振る舞いが予想通りであることを示しています。
1980年代のモジュラー性との関連: 楕円曲線とモジュラー形式の関係が深く研究され、谷山志村予想（後のワイルズによるフェルマーの最終定理の証明）と結びつくことがわかりました。この発見は、BSD予想の解析的側面を強化するものでした。
2000年代の数値検証: コンピュータを用いた大規模な数値計算により、多くの楕円曲線に対してBSD予想が正しいことが確認されました。特に、ランクが高い場合の例も見つかり、予想の普遍性が支持されています。

5.2 未解決部分

一方で、BSD予想の完全な証明は未だに達成されていません。主な課題は以下の通りです。

一般的な楕円曲線への適用: 現在の結果は特定のクラスに限定されており、任意の楕円曲線に対してBSD予想を証明するには、新たな数学的手法が必要です。
L関数の厳密な解析:
$s = 1$ におけるL関数の振る舞いを理論的に予測することは困難であり、特に高次の零点の次数をランクと一致させる証明が求められています。
ランクの上限: 楕円曲線のランクに理論的な上限があるかどうか不明です。現在の記録では、ランクが28の楕円曲線が発見されていますが、これが最大かどうかはわかっていません。

これらの未解決部分を克服するためには、数論、代数幾何学、解析学の融合が不可欠であり、次世代の数学者に大きな挑戦を与えています。

6. BSD予想の意義と展望

6.1 数学的意義

BSD予想が証明されれば、楕円曲線の有理点の構造が完全に解析的手法で解明されることになります。これは、フェルマーの最終定理の証明に匹敵する歴史的な成果となり、数論の基礎理論に新たな光を投じることでしょう。また、楕円曲線は現代暗号理論（例: 楕円曲線暗号）の基盤ともなっているため、BSD予想の解決は応用数学にも影響を及ぼします。