ループ量子重力理論(Loop Quantum Gravity, LQG)とは?
ループ量子重力理論(Loop Quantum Gravity, 以下 LQG)は、重力を量子論的に記述することを目的とした理論です。一般相対性理論と量子力学を統合する「量子重力理論」の代表的アプローチの一つであり、特に次の2点に大きな特徴があります。
- 時空そのものを量子化する
- 背景となる時空を仮定しない(背景独立性)
LQGでは、プランクスケール(約 10⁻³⁵ m)において、時空は連続的ではなく離散的な構造を持つと考えます。この離散構造は、後述する「スピンネットワーク」によって数学的に記述されます。
量子重力理論の必要性
20世紀の物理学は、一般相対性理論と量子力学という二つの偉大な理論を生み出しました。一般相対性理論は、重力を時空の曲がりとして記述し、巨視的なスケールでの宇宙の構造や天体現象を見事に説明します。一方、量子力学は、素粒子や原子といったミクロな世界を支配する法則を与えてくれます。
しかし、これら二つの理論は互いに相容れない側面を持っています。一般相対性理論は決定論的で連続的な時空を前提とするのに対し、量子力学は確率論的で離散的なエネルギー準位を特徴とします。通常のスケールではこの矛盾は問題になりませんが、ブラックホールの中心や宇宙の誕生直後のような極限的な状況では、重力も量子論的に扱わなければなりません。
量子重力理論が必要とされる代表的な状況として、以下が挙げられます。
ブラックホールの特異点: 一般相対性理論では、ブラックホールの中心で曲率が無限大に発散する特異点が現れます。これは理論が破綻していることを示唆しており、量子効果を取り入れることで解決が期待されます。
ビッグバン特異点: 宇宙の始まりにおいても、密度とエネルギーが無限大となる特異点が現れます。量子重力理論は、この特異点を回避し、宇宙の真の起源を明らかにする可能性を秘めています。
プランクスケールの物理: プランク長(約10⁻³⁵ m)やプランク時間(約10⁻⁴³秒)といった極微小スケールでは、量子的な時空の揺らぎが無視できなくなります。
一般相対性理論のハミルトン形式とアシュテカル変数

LQGの出発点は、一般相対性理論をハミルトン形式で再定式化することです。通常、重力はメトリックテンソル gμν によって表されますが、これを直接量子化することは非常に困難です。
そこで導入されるのがアシュテカル変数(Ashtekar variables)です。これは、一般相対性理論を SU(2) ゲージ理論の形に書き換えるための変数です。
基本変数
- \(A_a^i\):アシュテカル接続(SU(2) ゲージ場)
- \(E^a_i\):面積密度(電場に類似)
- \(\Gamma_a^i\):スピン接続
- \(K_a^i\):外部曲率
- \(\beta\):バリアーベル=インミルツィ・パラメータ
この書き換えにより、重力は電磁気学や量子色力学と同様の枠組みで量子化できるようになります。
ハミルトン形式の利点
ハミルトン形式では、時空を空間と時間に分割し、時間発展を記述する制約条件を明示的に扱います。一般相対性理論のハミルトン形式は、ADM形式(Arnowitt-Deser-Misner formalism)として知られていますが、アシュテカル変数を用いることで、より扱いやすい形になります。
特に重要なのは、この形式により重力理論がゲージ理論の構造を持つことが明確になる点です。電磁気学がU(1)ゲージ理論、強い相互作用がSU(3)ゲージ理論であるのと同様に、重力はSU(2)(または複素化するとSL(2,C))のゲージ理論として理解できるのです。
制約条件
一般相対性理論をハミルトン形式で書くと、いくつかの制約条件が現れます。
ガウス制約: SU(2)ゲージ対称性を表す制約で、各点でのゲージ不変性を要求します。
ベクトル制約(空間微分同相制約): 空間座標の再パラメータ化に対する不変性を表します。
スカラー制約(ハミルトン制約): 時間座標の再パラメータ化に対する不変性を表し、時空の動力学を支配します。
これらの制約条件を量子論的に課すことが、LQGの重要な課題の一つです。
ループ量子重力の量子化手法
LQGでは、場を点で扱うのではなく、積分量を基本変数とします。これにより、連続的な時空を仮定せずに量子化が可能となります。
ホロノミー
曲線 e に沿ったホロノミーは次のように定義されます。
ここで P は経路順序積を表します。
ホロノミーは、曲線に沿って接続を積分した量であり、その曲線における「平行移動」を表します。ゲージ理論では、ホロノミーはゲージ不変な物理量を構成する基本的な要素となります。
フラックス
面 S を貫くフラックスは次式で与えられます。
これらを用いて、時空の量子的な状態が構成されます。
フラックスは、面を貫く「電場」に類似した量であり、ホロノミーと正準共役な関係にあります。古典論におけるポアソン括弧が、量子論では交換関係に置き換わり、ホロノミーとフラックスの交換関係が基本的な量子化条件を与えます。
ループ表現
LQGの名前の由来でもある「ループ」は、閉曲線に沿ったホロノミーのトレースを取ったウィルソンループから来ています。初期のアプローチでは、これらのウィルソンループを基底として波動関数を展開しましたが、後にスピンネットワークと呼ばれるより一般的な状態表現が発見されました。
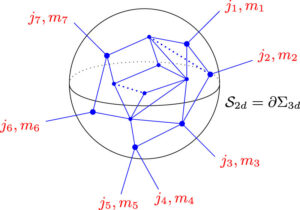
スピンネットワークと離散的時空
https://www.researchgate.net/figure/Loop-quantum-gravity-boundary-data-defined-by-the-spin-network-puncturing-the_fig1_351792075
LQGにおける量子状態はスピンネットワークと呼ばれるグラフで表されます。スピンネットワークは、以下の要素から構成されます。
- エッジ:SU(2) のスピン量子数 j でラベル付けされた線分
- ノード:エッジの結合条件(インターツイナー)でラベル付けされた頂点
スピンネットワークは、量子化された幾何学を表現する数学的対象です。各エッジは量子化された面積を表し、各ノードは量子化された体積を表します。
面積の量子化
面積演算子の固有値は次の式で与えられます。
ここで l_p はプランク長です。この式は、面積が離散値を取ることを示しています。
これは驚くべき結果です。古典的には、面積は連続的にどんな値でも取れると考えられていましたが、量子重力理論では、面積には最小単位が存在し、それはプランク長の二乗のオーダーなのです。
体積の量子化
https://www.treehugger.com/what-is-quantum-foam-4862885
同様に、体積演算子の固有値も離散的な値を取ります。ノードに付随する体積は、そのノードに接続するエッジのスピン量子数によって決まります。計算は複雑ですが、やはりプランク長の三乗のオーダーの離散値となります。
スピンフォーム
スピンネットワークは、ある時刻における空間の量子状態を表しますが、時間発展を含めた4次元時空の量子状態を記述するには、スピンフォームと呼ばれるより一般的な構造が必要です。スピンフォームは、スピンネットワークの時間発展の履歴として理解できます。
スピンフォームは、4次元の単体分割(triangulation)上で定義され、
- 面:スピン量子数でラベル付け
- エッジ:インターツイナーでラベル付け
- 頂点:遷移振幅でラベル付け
されます。スピンフォームアプローチは、LQGの共変的(covariant)な定式化を与え、時空の量子的な振幅を計算する枠組みを提供します。
ブラックホールとループ量子重力
ブラックホールのエントロピー
ベッケンシュタイン=ホーキングのエントロピーは
と表されます。LQGでは、事象の地平線を貫くスピンネットワークの状態数を数えることで、この式を微視的に導出できます。
具体的には、地平線を面と見なし、その面を貫くスピンネットワークのエッジの数とスピン量子数の組み合わせを数えます。バリアーベル=インミルツィ・パラメータ β の値を適切に選ぶと(β = ln2/(π√3) 程度)、ベッケンシュタイン=ホーキングの公式が正確に再現されます。
この結果は、LQGの最も重要な成功の一つとされています。ブラックホールのエントロピーが、実際には地平線の微視的な量子状態の数に由来することを示したからです。
ホーキング放射との関係
ホーキング放射は、ブラックホールが量子効果により粒子を放出し、徐々に蒸発していく現象です。LQGの枠組みでホーキング放射を完全に導出することは、まだ完全には達成されていませんが、いくつかの研究が進められています。
特に、地平線近傍での量子揺らぎや、トンネル効果を通じた粒子生成のメカニズムが、スピンネットワークの枠組みで研究されています。
特異点の回避
LQGでは、時空が離散的であるため、ブラックホール中心の特異点は無限大に発散せず、量子バウンスによって回避される可能性があります。
具体的には、ブラックホールの内部構造を記述する際、古典論では曲率が無限大になる点で理論が破綻しますが、LQGでは離散的な量子状態の遷移として記述されるため、曲率には自然な上限が生じます。これにより、特異点は「量子的に滑らかな」領域に置き換えられると考えられています。
一部のモデルでは、ブラックホールの中心部で時空が「反転」し、別の領域(ホワイトホールや別の宇宙)につながる可能性も示唆されています。
ループ量子宇宙論(LQC)

LQGを宇宙論に適用した理論がループ量子宇宙論(Loop Quantum Cosmology, LQC)です。
ビッグバン特異点の解消
LQCでは、宇宙は
収縮 → 量子バウンス → 膨張
という過程を経ると考えられ、ビッグバン特異点は回避されます。
古典的な宇宙論では、時間を過去に遡ると、宇宙の密度とエネルギーが無限大になるビッグバン特異点に到達します。しかし、LQCでは、密度がプランク密度に近づくと量子効果が顕著になり、重力が斥力的に働き始めます。これにより、宇宙は特異点に到達せず、「バウンス」して膨張に転じるのです。
インフレーションとの関係
宇宙の初期膨張を説明する標準的な理論であるインフレーション理論と、LQCがどのように関係するかは、活発に研究されているテーマです。
一部のモデルでは、量子バウンスの後に自然にインフレーション的な膨張期が現れることが示されています。また、LQCの効果により、初期宇宙の揺らぎのスペクトルに特徴的な修正が加わる可能性があり、これは将来の宇宙マイクロ波背景放射の精密観測によって検証できるかもしれません。
宇宙の前史
量子バウンスのシナリオでは、現在の膨張宇宙の前に、収縮していた「前宇宙」が存在したことになります。この前宇宙の性質や、どのような情報が量子バウンスを経て現在の宇宙に引き継がれるかは、興味深い研究テーマです。
一般には、古典的な情報の多くはバウンス時に失われますが、ある種の量子的な相関は保存される可能性があります。
超弦理論との比較
量子重力理論のもう一つの有力候補である超弦理論と、LQGはしばしば比較されます。
超弦理論は、素粒子を点ではなく1次元の「弦」として扱い、その振動モードが異なる素粒子に対応すると考えます。超弦理論は10次元や11次元の高次元時空を必要とし、余剰次元がコンパクト化されることで、我々の4次元時空が現れると説明します。
一方、LQGは、余剰次元を仮定せず、4次元時空の幾何学そのものを量子化します。また、超弦理論が背景時空を必要とするのに対し、LQGは背景独立な理論です。
それぞれの理論には長所と短所があります。
超弦理論の長所:
- 素粒子の統一的記述が可能
- ゲージ理論と重力を自然に含む
- 数学的に豊かな構造
超弦理論の短所:
- 背景時空に依存
- 多数の真空状態(ランドスケープ問題)
- 実験的検証が困難
LQGの長所:
- 背景独立
- 4次元時空で完結
- ブラックホールエントロピーの導出
LQGの短所:
- 素粒子の統一的記述が未完成
- 低エネルギー極限での一般相対性理論の再現が自明でない
- 実験的検証が困難
近年、両理論の関係性を探る研究も進められており、将来的には統合される可能性も示唆されています。
実験的検証の可能性
量子重力効果はプランクスケールで顕著になるため、直接的な実験検証は極めて困難です。しかし、いくつかの間接的な検証方法が提案されています。
光速の分散関係の修正
LQGの一部のモデルでは、光速が微小にエネルギー依存する可能性が予測されます。これは、時空の離散構造に起因する効果です。
遠方のガンマ線バースト(GRB)からの光を観測し、異なるエネルギーの光子の到達時間差を測定することで、この効果を検証できる可能性があります。ただし、現在の観測精度では、明確な結果は得られていません。
宇宙マイクロ波背景放射
LQCの効果は、宇宙マイクロ波背景放射(CMB)の温度揺らぎのパターンに特徴的な痕跡を残す可能性があります。将来の高精度観測により、これらの痕跡を検出できるかもしれません。
ブラックホール観測
ブラックホールの合体時に放出される重力波の詳細な分析により、事象の地平線近傍での量子重力効果を探ることができる可能性があります。また、ブラックホールシャドウの精密観測も、情報を提供するかもしれません。
課題と今後の展望
LQGは理論的に非常に魅力的ですが、以下のような課題が残されています。
実験的検証の困難さ
前述の通り、プランクスケールの物理を直接観測することは現在の技術では不可能です。理論の予測と観測可能な現象を結びつける、より具体的なシナリオの開発が必要です。
低エネルギー極限
LQGから低エネルギー極限として一般相対性理論が正確に再現されることを示すことは、理論の整合性にとって重要ですが、完全には証明されていません。特に、ハミルトン制約の量子化には曖昧さがあり、適切な制約を課すことが技術的に困難です。
物質との結合
LQGは重力の量子化に焦点を当てていますが、標準模型の素粒子をLQGの枠組みに自然に組み込むことは、まだ完全には達成されていません。物質場とスピンネットワークがどのように相互作用するかの詳細な理解が必要です。
他理論との関係
超弦理論との関係、あるいは他の量子重力アプローチ(因果的動的三角形分割、非可換幾何学など)との関連性を明らかにすることは、量子重力理論全体の理解を深める上で重要です。
パラメータ β の理論的決定
バリアーベル=インミルツィ・パラメータ β は、理論の重要なパラメータですが、現在のところ、ブラックホールエントロピーの正確な値を再現するように現象論的に決定されています。この値を理論的な第一原理から導出することが望まれます。
最近の発展
近年、LQG研究にはいくつかの重要な進展がありました。
スピンフォーム振幅の計算
スピンフォームアプローチを用いて、簡単な時空の遷移振幅を数値的に計算する手法が発展してきました。これにより、量子時空の動力学をより具体的に理解できるようになりつつあります。
テンソルネットワークとの関係
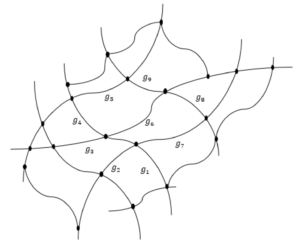
https://www.mdpi.com/physics/physics-04-00072/article_deploy/html/images/physics-04-00072-g001.png
凝縮系物理学で発展したテンソルネットワーク理論と、スピンネットワークの間に深い関係があることが明らかになってきました。これにより、両分野の技術を相互に応用できる可能性が開けています。
漸近的安全性との接点
量子重力のもう一つのアプローチである「漸近的安全性」の研究と、LQGの関係を探る研究も進められています。両者は異なる方法で時空の量子化に取り組んでいますが、共通する構造が見出されつつあります。
まとめ
ループ量子重力理論は、重力を量子化し、時空の離散構造を明らかにする革新的な理論です。ブラックホールや宇宙初期の問題に新たな視点を与えるこの理論は、量子重力研究の中核として今後も重要な役割を果たすでしょう。
LQGの最大の魅力は、時空そのものを動的な量子的対象として扱う点にあります。連続的で滑らかな時空という古典的描像を超えて、プランクスケールでは時空が離散的なスピンネットワークとして記述されるという斬新な描像は、物理学の根本的な問いに新しい答えを与える可能性を秘めています。
実験的検証の困難さや理論的課題は残されていますが、数学的な厳密性と物理的な洞察を兼ね備えたLQGは、21世紀の理論物理学における最も挑戦的で刺激的な研究分野の一つであり続けるでしょう。将来、観測技術の進歩や理論的ブレークスルーにより、量子重力の真の姿が明らかになる日を、多くの研究者が期待しています。



