
1. F理論とは何か?
F理論(F-theory)は、超弦理論(Superstring Theory)の枠組みをさらに拡張した先進的な理論物理学のモデルであり、1990年代中盤にエドワード・ウィッテン(Edward Witten)やクムラン・ヴァッファ(Cumrun Vafa)などの著名な理論物理学者によって提唱されました。この理論は、従来の10次元超弦理論を12次元ではなく11次元やそれに相当する時空で記述することで、重力と量子力学を含むすべての基本相互作用を統一した究極の理論(Theory of Everything)を構築することを目指しています。特に、カラビ・ヤウ空間(Calabi-Yau manifold)と呼ばれる高度に複雑な幾何学構造を活用し、時空の微細な構造や基本的な物理法則を純粋に数学的な観点から詳細に記述するのが大きな特徴です。これにより、粒子物理学や宇宙論の未解決問題に新たな光を当てる可能性を秘めています。
F理論の名称は、時には「Father(父)」や「Fiber(ファイバー)」に由来すると冗談めかして言われることがありますが、実際には特定の深い意味を持つものではなく、研究者たちが当時の理論の流れの中で便宜的に命名したものです。この理論は、超弦理論の5つの異なるバージョン(I型、IIA型、IIB型、ヘテロティックSO(32)、ヘテロティックE₈×E₈)を一つの統一された枠組みで扱うことを可能にし、M理論との強い関連性も持っています。理論物理学の最前線で長年注目を集め続け、弦理論の非摂動的効果を扱う強力なツールとして位置づけられています。
M理論とは何か?超弦理論を統合する究極の理論とは?M理論について徹底解説
1.1 超弦理論との関係
超弦理論は、宇宙の根本を時間1次元+空間9次元、合計10次元の時空で記述する革新的な理論です。この10次元時空は、私たちが日常的に体験する3次元空間(長さ、幅、高さ)と1次元時間に加え、残りの6次元が「余剰次元」として極めて小さなスケールでコンパクト化(巻き付いて丸まる)された形で存在すると仮定されています。この余剰次元はプランク長(約10⁻³⁵メートル)程度の極微小なサイズのため、現在の実験技術では直接観測できず、間接的な影響としてのみ現れると考えられています。
F理論は、この超弦理論をさらに発展させ、効果的に11次元(または12次元相当)の視点を取り入れることで、より包括的な記述を可能にします。この追加の次元は物理的に実在するものではなく、「仮想的な次元」として数学的に導入され、幾何学的な構造を柔軟に扱うための便利な道具です。このアプローチはM理論(M-theory)と非常に密接に関連しており、M理論が11次元超重力理論を基盤とするのに対し、F理論は特にIIB型超弦理論の非摂動的(強い結合領域の)側面を楕円曲線を用いた幾何学で表現します。これにより、異なる弦理論間の双対性(duality)を明確に示すことができ、理論の統一性を強化しています。
1.2 F理論の目的と意義
F理論の主要な目的は、超弦理論の5つの異なるタイプを一つの枠組みで統一し、重力、電磁気力、弱い核力、強い核力を含むすべての力を量子レベルで統合することです。特に、IIB型超弦理論のSL(2,Z)対称性を活用した非摂動的効果を扱う点で優れており、標準模型(Standard Model)のゲージ群や粒子スペクトルを幾何学的に自然に導出する可能性を秘めています。また、宇宙論的な問題、例えばインフレーションのメカニズムやブラックホールの性質、さらには暗黒エネルギーや暗黒物質の起源にも応用が期待され、現象論的なモデル構築で積極的に用いられています。この理論は、弦理論の「風景(landscape)」問題、つまり膨大な数の可能な真空状態を整理する上でも重要な役割を果たします。
2. F理論の数学的基盤
F理論を深く理解するためには、複素幾何学(complex geometry)、代数幾何学(algebraic geometry)、さらには微分幾何学の高度な知識が不可欠です。特に、楕円曲線(elliptic curve)とカラビ・ヤウ空間が理論の核心を形成し、これらの構造が11次元時空の幾何学的表現を提供します。これにより、物理的な量が純粋に数学的な性質から決定されるという美しい対応が生まれます。
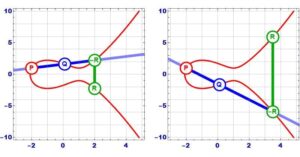
2.1 楕円曲線とは?
https://www.allaboutcircuits.com/technical-articles/elliptic-curve-cryptography-in-embedded-systems/
楕円曲線は、代数幾何学において重要な曲線であり、以下のような三次方程式で定義されます。
ここで、
は定数であり、曲線が非特異(滑らか)であるためには、判別式が次の条件を満たす必要があります。
この判別式が0でないことは、曲線が特異点(例えば、尖点や交点)を持たないことを保証します。楕円曲線は、複素平面上でトーラス(ドーナツ型)の形状を持ち、F理論では時空の各点にこのような楕円曲線を対応させることで、11次元時空の幾何学を構築します。この対応は、ファイバー構造(fiber structure)として知られ、時空の各点に楕円曲線を「ファイバー」として付加するイメージです。
2.2 カラビ・ヤウ空間とF理論

カラビ・ヤウ空間は、超弦理論やF理論で余剰次元を記述するために用いられる複雑な幾何学的構造です。具体的には、リッチ平坦(Ricci-flat)な複素多様体であり、コンパクト化された6次元空間を表現します。F理論では、このカラビ・ヤウ空間に楕円曲線をファイバーとして持つ構造(楕円ファイブレーション、elliptic fibration)を考えます。この構造により、10次元のIIB型超弦理論を11次元で再解釈し、さらなる物理的現象を説明することが可能になります。
カラビ・ヤウ空間の選択は、ゲージ群や粒子の世代数(例えば、クォークやレプトンの種類)に直接影響を与えます。F理論では、この空間の特異点やファイバーの縮退(degeneration)が、物理的な粒子の性質や相互作用を決定する重要な要素となります。
2.3 モジュライ空間とタウ関数
F理論では、IIB型超弦理論のタウ関数(τ)が重要な役割を果たします。このタウ関数は、以下のように定義されます。
ここで、
は楕円関数であり、複素平面上のモジュライ空間(moduli space)を記述します。タウ関数の値は、時空の各点で変化し、これがF理論の幾何学的構造や物理的性質を決定します。特に、タウ関数の空間依存性は、Dブレーンやゲージ場の振る舞いと密接に関連しています。
3. 物理的な解釈

F理論は、Dブレーン(D-brane)と呼ばれる高次元の膜構造を導入することで、物理的な現象を説明します。Dブレーンは、超弦理論において弦の端点が付着する高次元物体であり、ゲージ理論や重力の相互作用を記述する重要な要素です。F理論では、これらのDブレーンがカラビ・ヤウ空間の特異点に対応し、標準模型のゲージ群(SU(3) × SU(2) × U(1))や粒子の性質を自然に導出します。
3.1 Dブレーンとゲージ理論
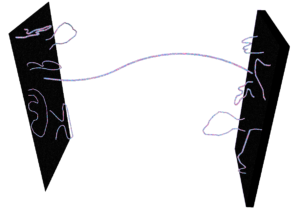
https://en.wikipedia.org/wiki/D-brane
Dブレーンは、超弦理論においてゲージ場(例えば、電磁場や強い相互作用を記述する場)の起源と考えられます。F理論では、D7ブレーンと呼ばれる7次元のブレーンが特に重要です。これらのブレーンは、時空の特定の点で楕円曲線が縮退する場所に現れ、ゲージ群の構造を決定します。例えば、SU(3)(強い相互作用)、SU(2)(弱い相互作用)、U(1)(電磁相互作用)のゲージ群は、D7ブレーンの配置や特異点の性質から導かれます。
3.2 ブラックホールとエントロピー
F理論は、ブラックホールのエントロピーや情報問題にも応用可能です。超弦理論では、Dブレーンを用いてブラックホールの微視的状態を記述し、そのエントロピー(熱力学的乱雑さの指標)を計算することができます。F理論では、さらに高次元の視点からブラックホールの性質を分析し、情報パラドックス(ブラックホールに落ちた情報が失われるかどうか)の解決に新たな視点を提供します。
3.3 宇宙論とインフレーション
F理論は、宇宙の初期状態やインフレーション(急激な膨張)のメカニズムを説明する可能性も持っています。カラビ・ヤウ空間のモジュライ(形状やサイズを決定するパラメータ)が時間とともに変化することで、宇宙の膨張や暗黒エネルギーの起源を記述できる可能性があります。また、F理論の枠組みでは、暗黒物質やニュートリノの質量など、標準模型では説明しきれない現象についても新たな洞察が得られるかもしれません。
4. F理論の応用
F理論は、理論物理学の多くの未解決問題にアプローチするための強力なツールです。以下に、主要な応用例を詳しく見ていきます。
- 標準模型の自然な導出: F理論は、カラビ・ヤウ空間の特異点やファイバーの構造を通じて、標準模型のゲージ群(SU(3) × SU(2) × U(1))や粒子の世代数を自然に導出します。これは、素粒子の質量や相互作用の強さを説明する上で重要な成果です。
- ブラックホール情報問題: F理論は、ブラックホールのエントロピーやホーキング放射の微視的起源を説明する可能性があります。特に、Dブレーンを用いた計算により、ブラックホールの情報が失われないことを示唆する結果が得られています。
- 宇宙論への応用: F理論は、インフレーションや暗黒物質、暗黒エネルギーの起源を説明するモデルを提供します。例えば、カラビ・ヤウ空間のモジュライ場がインフレーションを駆動するポテンシャルを提供する可能性があります。
- 弦の風景(String Landscape): F理論は、超弦理論の「弦の風景」と呼ばれる膨大な数の真空状態を記述するツールとしても利用されます。これにより、宇宙の物理定数がなぜ現在の値を持つのかを説明する試みが行われています。
5. 例え話で理解するF理論
F理論の概念は抽象的で理解が難しいため、以下に直感的な例え話を用いて説明します。
5.1 2次元世界のアリ
2次元の平面に住むアリを想像してください。このアリは、上下左右(2次元)しか認識できません。もし3次元のボールがこの平面を通過すると、アリは以下のような現象を観察します。
- 最初に、ボールが平面に触れた瞬間、点が現れる。
- ボールがさらに通過すると、点が円に広がり、大きくなっていく。
- ボールが平面を離れると、円が縮小し、最終的に点に戻って消える。
アリにとって、この現象は理解しがたい「高次元の影響」です。同様に、私たちが3次元空間+1次元時間(4次元時空)に住んでいる中で、F理論の11次元は直接観測できない高次元の影響を記述します。
5.2 F理論の11次元
F理論の11次元は、私たちの4次元時空にコンパクト化された7次元の余剰次元が加わったものです。これらの余剰次元は、カラビ・ヤウ空間として丸まっており、非常に小さなスケールで存在します。例え話で言えば、私たちがアリのように「平面」に住んでいるのに対し、F理論は高次元の「ボール」の全体像を記述する理論です。この高次元構造が、素粒子の性質や宇宙の構造を決定しているのです。
5.3 日常生活へのアナロジー
もう一つの例えとして、インターネットのネットワークを考えてみましょう。私たちが普段使うインターネットは、2次元的な画面(ウェブページ)として見えますが、実際にはサーバーやケーブル、光ファイバーといった「見えない次元」が裏で働いています。F理論の余剰次元も、日常の物理現象の背後に隠れた構造として機能し、宇宙の法則を支えていると考えることができます。
6. F理論の課題と今後の展望
F理論は、理論物理学の統一理論としての可能性を秘めていますが、いくつかの課題も存在します。まず、数学的構造が非常に複雑であり、カラビ・ヤウ空間や楕円曲線の詳細な解析には高度な計算技術が必要です。また、F理論が予測する高次元時空やDブレーンの存在を直接観測することは、現在の技術ではほぼ不可能です。そのため、F理論の検証は間接的な方法、例えば粒子加速器での実験や宇宙背景放射の観測に頼っています。
しかし、F理論は多くの可能性を開く理論でもあります。例えば、LHC(大型ハドロン衝突型加速器)や次世代の宇宙望遠鏡による観測データが、F理論の予測を裏付ける証拠を提供するかもしれません。また、量子コンピュータの発展により、カラビ・ヤウ空間のシミュレーションが可能になり、F理論の数学的構造をより詳細に探る道が開けるかもしれません。
7. まとめ
F理論は、超弦理論を拡張した11次元時空の理論であり、楕円曲線やカラビ・ヤウ空間を基盤として、物理法則の統一を目指しています。Dブレーンやタウ関数を通じて、標準模型のゲージ群やブラックホールの性質、宇宙の膨張などを自然に記述する可能性を持ちます。数学的には高度で複雑ですが、例え話を用いることで直感的な理解も可能です。今後の研究により、F理論が現実の物理現象とどのように結びつくのかが明らかになることが期待されます。
F理論は、理論物理学の最前線に位置する挑戦的な理論であり、宇宙の根本的な構造を解き明かす鍵となるかもしれません。私たちの宇宙がどのように成り立っているのか、その謎を解くための重要な一歩として、F理論の研究は今後も注目されるでしょう。



